链表

May 02, 2022 3014

如何实现LRU缓存淘汰算法?

缓存是一种提高数据读取性能的技术，在硬件设计、软件开发中都有着非常广泛的应用，比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等。

缓存的大小有限，当缓存被用满时，哪些数据应该被清理出去，哪些数据应该被保留？这就需要缓存淘汰策略来决定。常见的策略有三种：

  1. 先进先出策略 FIFO（First In，First Out）
  2. 最少使用策略 LFU（Least Frequently Used）
  3. 最近最少使用策略 LRU（Least Recently Used）

数组与链表的对比

底层的存储结构

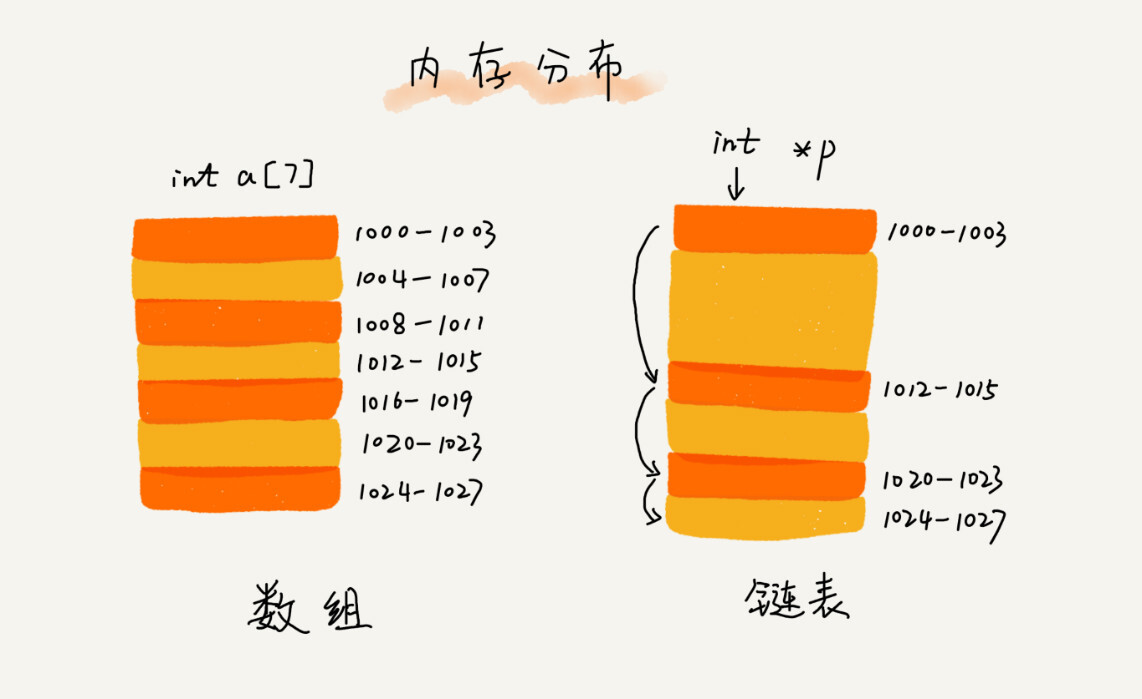
数组需要一块连续的内存空间来存储，对内存的要求比较高。

链表并不需要一块连续的内存空间，它通过“指针”将一组零散的内存块串联起来使用。把内存块称为链表的“结点”。

常见的链表结构

  1. 单链表

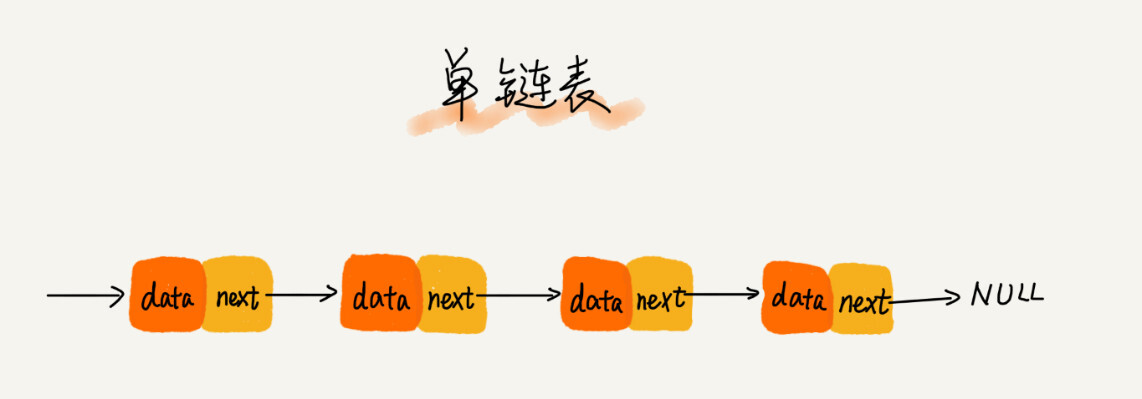
    单链表是一种链式存取的数据结构，用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的，每个结点的构成：元素(数据元素的映象) +指针(指示后继元素存储位置)，元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。

    有两个结点是比较特殊的

    1. 第一个结点叫作头结点，头结点用来记录链表的基地址，有了它，我们就可以遍历得到整条链表。
    2. 最后一个结点叫作尾结点。尾结点特殊的地方是：指针不是指向下一个结点，而是指向一个空地址 NULL，表示这是链表上最后一个结点。

    在进行数组的插入、删除操作时，为了保持内存数据的连续性，需要做大量的数据搬移，所以时间复杂度是 O(n)。而在链表中插入或者删除一个数据，我们并不需要为了保持内存的连续性而搬移结点，因为链表的存储空间本身就不是连续的。

    针对链表的插入和删除操作，我们只需要考虑相邻结点的指针改变，所以对应的时间复杂度是 O(1)。

    链表不能随机访问第 k 个元素。

    因为链表中的数据并非连续存储的，所以无法像数组那样，根据首地址和下标，通过寻址公式就能直接计算出对应的内存地址，而是需要根据指针一个结点一个结点地依次遍历，直到找到相应的结点。

    链表随机访问的性能没有数组好，需要 O(n) 的时间复杂度。

  2. 循环链表

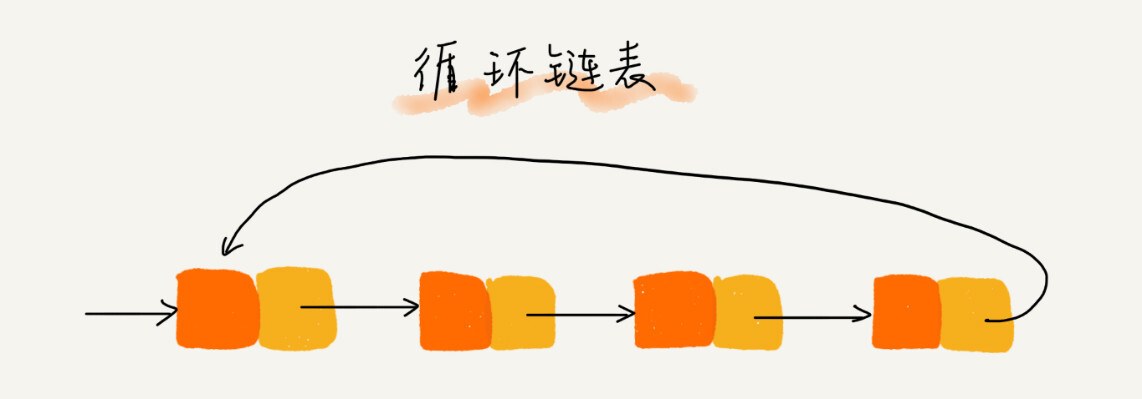
    循环链表是一种特殊的单链表，它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。

    和单链表相比，循环链表的优点是从链尾到链头比较方便。当要处理的数据具有环型结构特点时，就特别适合采用循环链表。

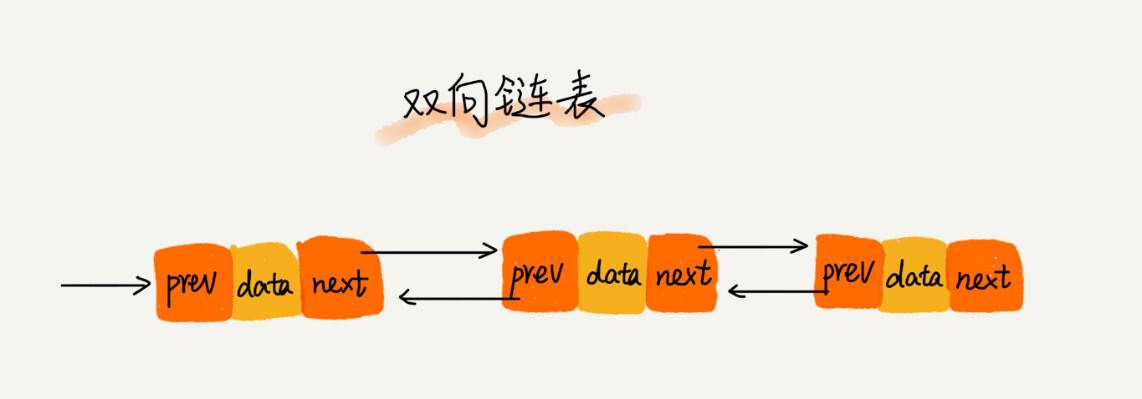
  3. 双向链表

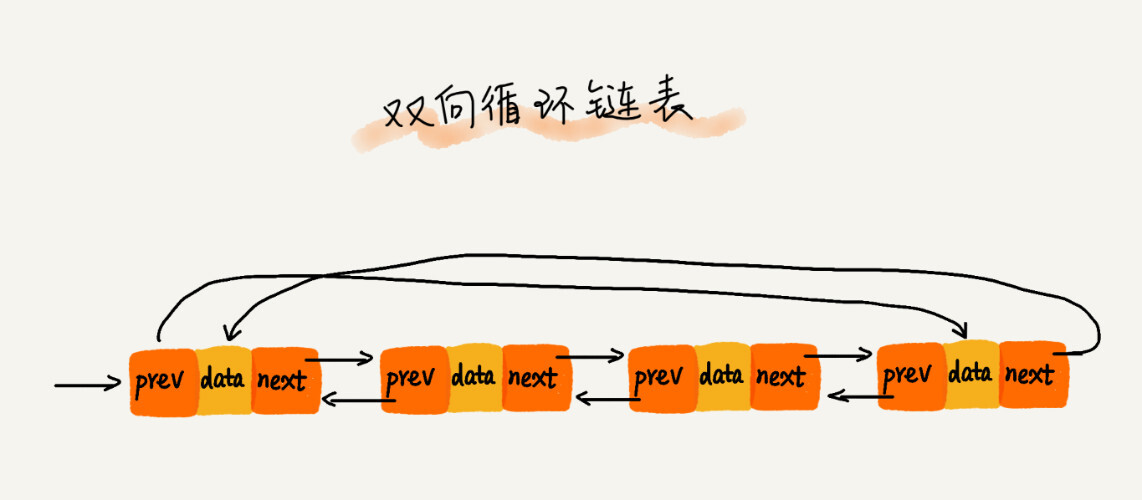
    双向链表也叫双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。

    双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以，如果存储同样多的数据，双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间，但可以支持双向遍历，这样也带来了双向链表操作的灵活性。

    双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点，正是这样的特点，也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效

    删除操作

    1. 删除结点中“值等于某个给定值”的结点；

      不管是单链表还是双向链表，为了查找到值等于给定值的结点，都需要从头结点开始一个一个依次遍历对比，直到找到值等于给定值的结点，然后再通过我前面讲的指针操作将其删除。

      尽管单纯的删除操作时间复杂度是 O(1)，但遍历查找的时间是主要的耗时点，对应的时间复杂度为 O(n)。根据时间复杂度分析中的加法法则，删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)。

    2. 删除给定指针指向的结点。

      单链表：已经找到了要删除的结点，但是删除某个结点 q 需要知道其前驱结点，而单链表并不支持直接获取前驱结点，所以，为了找到前驱结点，我们还是要从头结点开始遍历链表，直到 p->next=q，说明 p 是 q 的前驱结点。

      双链表：因为双向链表中的结点已经保存了前驱结点的指针，不需要像单链表那样遍历。单链表删除操作需要 O(n) 的时间复杂度，而双向链表只需要在 O(1) 的时间复杂度。

    插入操作

    在链表的某个指定结点前面插入一个结点，双向链表比单链表有很大的优势。双向链表需要 O(1) 时间复杂度，而单向链表需要 O(n) 的时间复杂度。

    按值查询

    对于一个有序链表，双向链表的按值查询的效率也要比单链表高一些。可以记录上次查找的位置 p，每次查询时，根据要查找的值与 p 的大小关系，决定是往前还是往后查找，所以平均只需要查找一半的数据。

用空间换时间的设计思想：当内存空间充足的时候，如果我们更加追求代码的执行速度，我们就可以选择空间复杂度相对较高、但时间复杂度相对很低的算法或者数据结构。

缓存实际上就是利用了空间换时间的设计思想。如果我们把数据存储在硬盘上，会比较节省内存，但每次查找数据都要询问一次硬盘，会比较慢。但如果我们通过缓存技术，事先将数据加载在内存中，虽然会比较耗费内存空间，但是每次数据查询的速度就大大提高了。

如何基于链表实现 LRU 缓存淘汰算法？

维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，我们从链表头开始顺序遍历链表。

  1. 如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
  2. 如果此数据没有在缓存链表中，又可以分为两种情况：
    1. 如果此时缓存未满，则将此结点直接插入到链表的头部；
    2. 如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

这种基于链表的实现思路，缓存访问的时间复杂度为 O(n)。

如何轻松写出正确的链表代码？

技巧一：理解指针或引用的含义

将某个变量赋值给指针，实际上就是将这个变量的地址赋值给指针，或者反过来说，指针中存储了这个变量的内存地址，指向了这个变量，通过指针就能找到这个变量。

技巧二：警惕指针丢失和内存泄漏

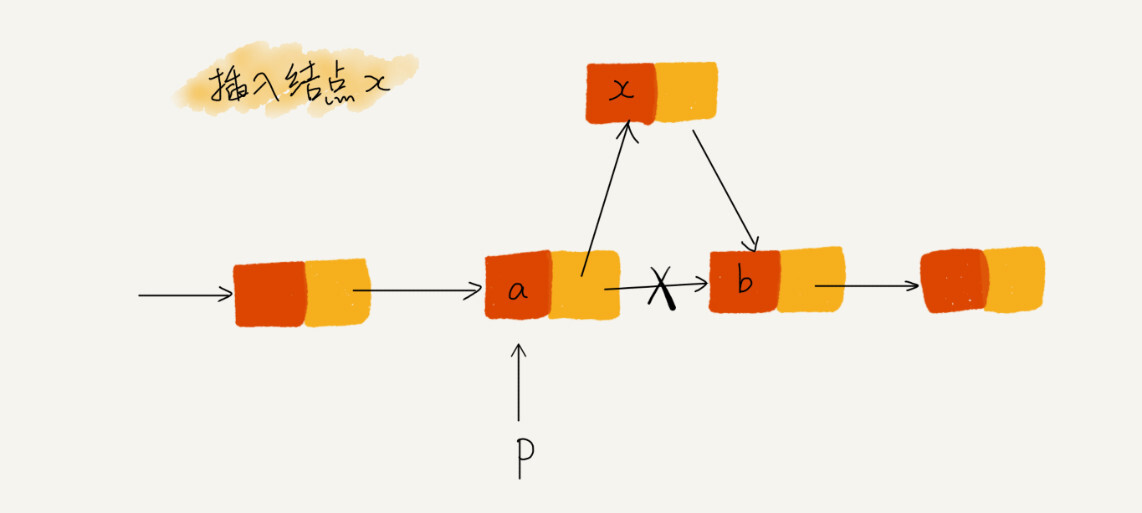
在结点 a 和相邻的结点 b 之间插入结点 x，假设当前指针 p 指向结点 a

将代码实现变成下面这个样子，就会发生指针丢失和内存泄露:

1
2
p->next = x;  // 将p的next指针指向x结点；
x->next = p->next;  // 将x的结点的next指针指向b结点；

p->next 指针在完成第一步操作之后，已经不再指向结点 b 了，而是指向结点 x。第 2 行代码相当于将 x 赋值给 x->next，自己指向自己。因此，整个链表也就断成了两半，从结点 b 往后的所有结点都无法访问到了。

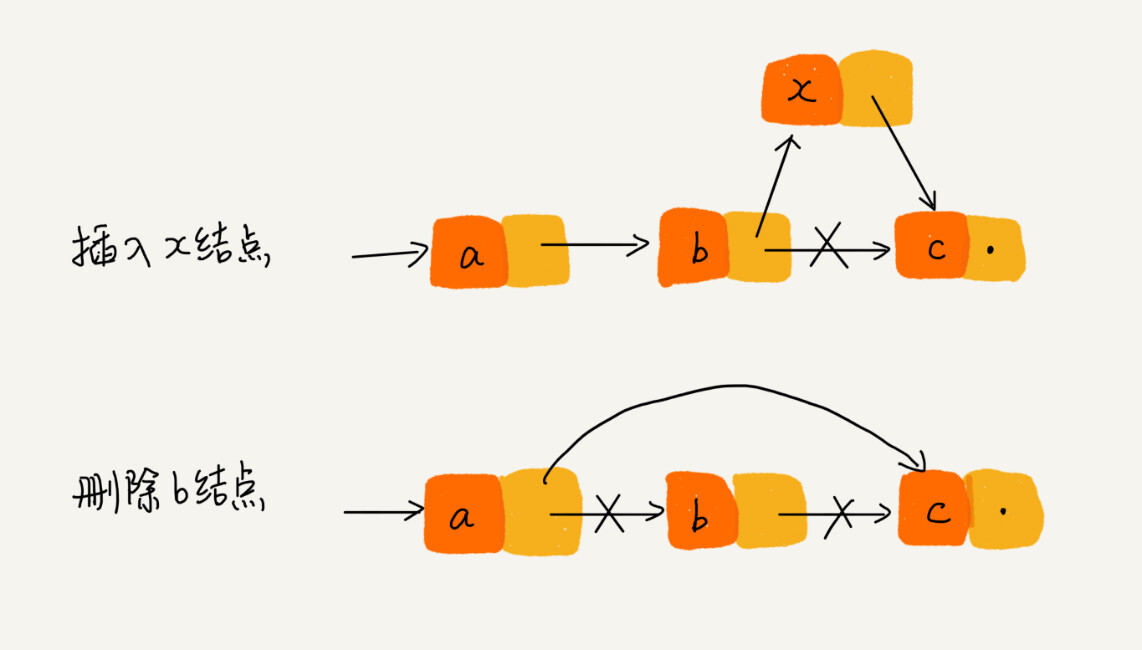
插入结点时，一定要注意操作的顺序

要先将结点 x 的 next 指针指向结点 b，再把结点 a 的 next 指针指向结点 x，这样才不会丢失指针，导致内存泄漏

删除链表结点时，也一定要记得手动释放内存空间

技巧三：利用哨兵简化实现难度

针对链表的插入、删除操作，需要对插入第一个结点和删除最后一个结点的情况进行特殊处理

引入哨兵结点，在任何时候，不管链表是不是空，head 指针都会一直指向这个哨兵结点。我们也把这种有哨兵结点的链表叫带头链表。相反，没有哨兵结点的链表就叫作不带头链表。

哨兵结点是不存储数据的

查看评论