分治算法

分治算法

分治算法（divide and conquer）的核心思想其实就是四个字，分而治之 ，也就是将原问题划分成 n 个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

分治算法是一种处理问题的思想，递归是一种编程技巧

分治算法的递归实现中，每一层递归都会涉及这样三个操作：

1. 分解：将原问题分解成一系列子问题；
2. 解决：递归地求解各个子问题，若子问题足够小，则直接求解；
3. 合并：将子问题的结果合并成原问题。

分治算法能解决的问题，一般需要满足下面这几个条件：

1. 原问题与分解成的小问题具有相同的模式；
2. 原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别；
3. 具有分解终止条件，也就是说，当问题足够小时，可以直接求解；
4. 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。

分治算法应用举例

如何求出一组数据的有序对个数或者逆序对个数

有序度来表示一组数据的有序程度，用逆序度表示一组数据的无序程度。

假设有 n 个数据，期望数据从小到大排列，那完全有序的数据的有序度就是 n(n-1)/2，逆序度等于 0；相反，倒序排列的数据的有序度就是 0，逆序度是 n(n-1)/2。

用分治的思想来求数组 A 的逆序对个数。可以将数组分成前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2，然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1+K2+K3。

归并排序中有一个非常关键的操作，就是将两个有序的小数组，合并成一个有序的数组。实际上，在这个合并的过程中，就可以计算这两个小数组的逆序对个数了。每次合并操作，都计算逆序对个数，把这些计算出来的逆序对个数求和，就是这个数组的逆序对个数了。

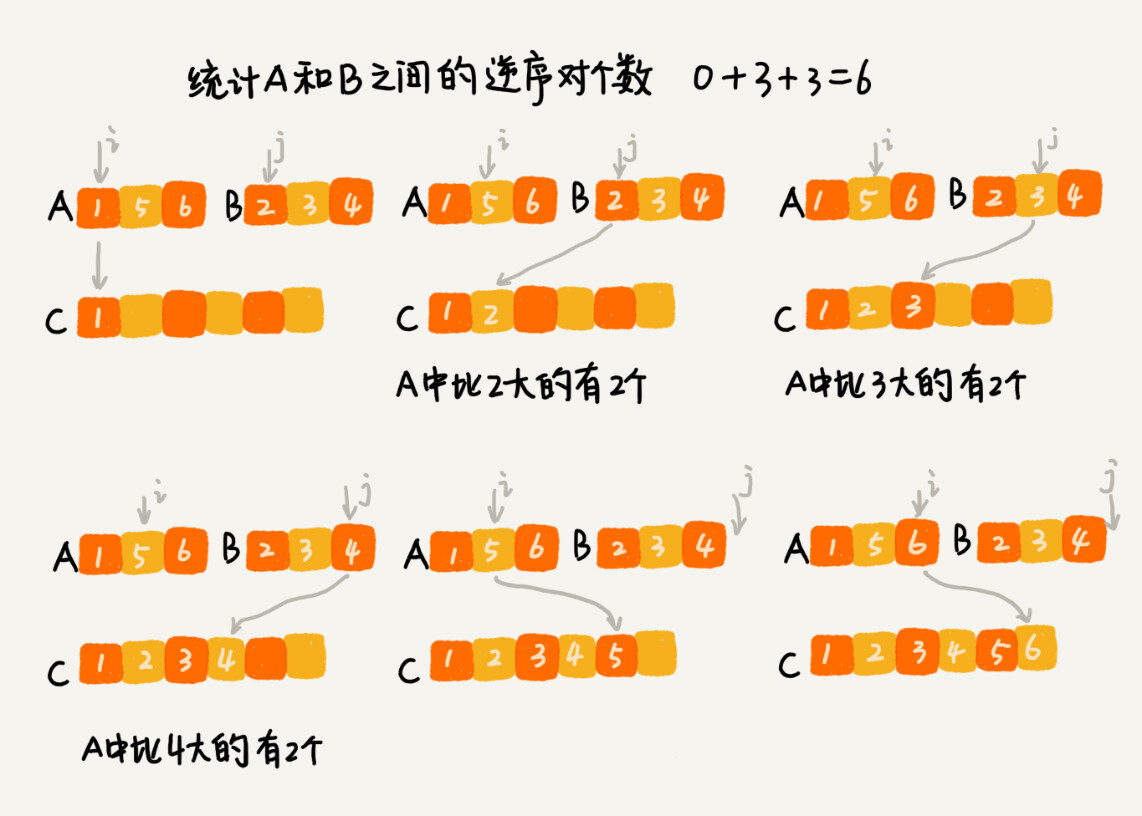
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

private int num = 0; // 全局变量或者成员变量

public int count(int[] a, int n) {
  num = 0;
  mergeSortCounting(a, 0, n-1);
  return num;
}

private void mergeSortCounting(int[] a, int p, int r) {
  if (p >= r) return;
  int q = (p+r)/2;
  mergeSortCounting(a, p, q);
  mergeSortCounting(a, q+1, r);
  merge(a, p, q, r);
}

private void merge(int[] a, int p, int q, int r) {
  int i = p, j = q+1, k = 0;
  int[] tmp = new int[r-p+1];
  while (i<=q && j<=r) {
    if (a[i] <= a[j]) {
      tmp[k++] = a[i++];
    } else {
      num += (q-i+1); // 统计p-q之间，比a[j]大的元素个数
      tmp[k++] = a[j++];
    }
  }
  while (i <= q) { // 处理剩下的
    tmp[k++] = a[i++];
  }
  while (j <= r) { // 处理剩下的
    tmp[k++] = a[j++];
  }
  for (i = 0; i <= r-p; ++i) { // 从tmp拷贝回a
    a[p+i] = tmp[i];
  }
}

分治思想在海量数据处理中的应用

给 10GB 的订单文件按照金额排序这样一个需求，看似是一个简单的排序问题，但是因为数据量大，有 10GB，而机器的内存可能只有 2、3GB ，无法一次性加载到内存，也就无法通过单纯地使用快排、归并等基础算法来解决了。

利用分治的思想。可以将海量的数据集合根据某种方法，划分为几个小的数据集合，每个小的数据集合单独加载到内存来解决，然后再将小数据集合合并成大数据集合。实际上，利用这种分治的处理思路，不仅仅能克服内存的限制，还能利用多线程或者多机处理，加快处理的速度。

给 10GB 的订单排序，可以先扫描一遍订单，根据订单的金额，将 10GB 的文件划分为几个金额区间。比如订单金额为 1 到 100 元的放到一个小文件，101 到 200 之间的放到另一个文件，以此类推。这样每个小文件都可以单独加载到内存排序，最后将这些有序的小文件合并，就是最终有序的 10GB 订单数据了。