位图

June 09, 2022 2060

位图

位图是通过将数组下标与应用中的一些值关联映射，数组中该下标所指定的位置上的元素可以用来标识应用中值的情况（是否存在或者数目 或者计数等），位图数组中每个元素在内存中占用1位，所以可以节省存储空间。位图是一种非常简洁快速的数据结构，它能同时使存储空间和速度最优化。

有 1 千万个整数，整数的范围在 1 到 1 亿之间。如何快速查找某个整数是否在这 1 千万个整数中呢？

可以使用一种比较“特殊”的散列表，那就是位图。

申请一个大小为 1 亿、数据类型为布尔类型（true 或者 false）的数组。
将这 1 千万个整数作为数组下标，将对应的数组值设置成 true。比如，整数 5 对应下标为 5 的数组值设置为 true，也就是 array[5]=true。

查询某个整数 K 是否在这 1 千万个整数中的时候，只需要将对应的数组值 array[K]取出来，看是否等于 true。如果等于 true，那说明 1 千万整数中包含这个整数 K；相反，就表示不包含这个整数 K。

很多语言中提供的布尔类型，大小是 1 个字节的，并不能节省太多内存空间。实际上，表示 true 和 false 两个值，只需要用一个二进制位（bit）就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class BitMap { // Java中char类型占16bit，也即是2个字节
  private char[] bytes;
  private int nbits;
  
  public BitMap(int nbits) {
    this.nbits = nbits;
    this.bytes = new char[nbits/16+1];
  }

  public void set(int k) {
    if (k > nbits) return;
    int byteIndex = k / 16;
    int bitIndex = k % 16;
    bytes[byteIndex] |= (1 << bitIndex);
  }

  public boolean get(int k) {
    if (k > nbits) return false;
    int byteIndex = k / 16;
    int bitIndex = k % 16;
    return (bytes[byteIndex] & (1 << bitIndex)) != 0;
  }
}

散列表是存储已有数据，而位图存储的是范围

比如有1、1000、1000000 ，散列表只需要存储三次，而位图首先需要1000000位才可以存储

问题：

如果数字的范围很大，数字范围不是 1 到 1 亿，而是 1 到 10 亿，那位图的大小就是 10 亿个二进制位，消耗内存就很大

解决方法：布隆过滤器

布隆过滤器

对位图这种数据结构的一种改进

数据个数是 1 千万，数据的范围是 1 到 10 亿

布隆过滤器的做法是，仍然使用一个 1 亿个二进制大小的位图，然后通过哈希函数，对数字进行处理，让它落在这 1 到 1 亿范围内。

比如把哈希函数设计成 f(x)=x%n。其中，x 表示数字，n 表示位图的大小（1 亿），也就是，对数字跟位图的大小进行取模求余。

问题：哈希函数会存在冲突

一个哈希函数可能会存在冲突，用多个哈希函数一块儿定位一个数据

布隆过滤器

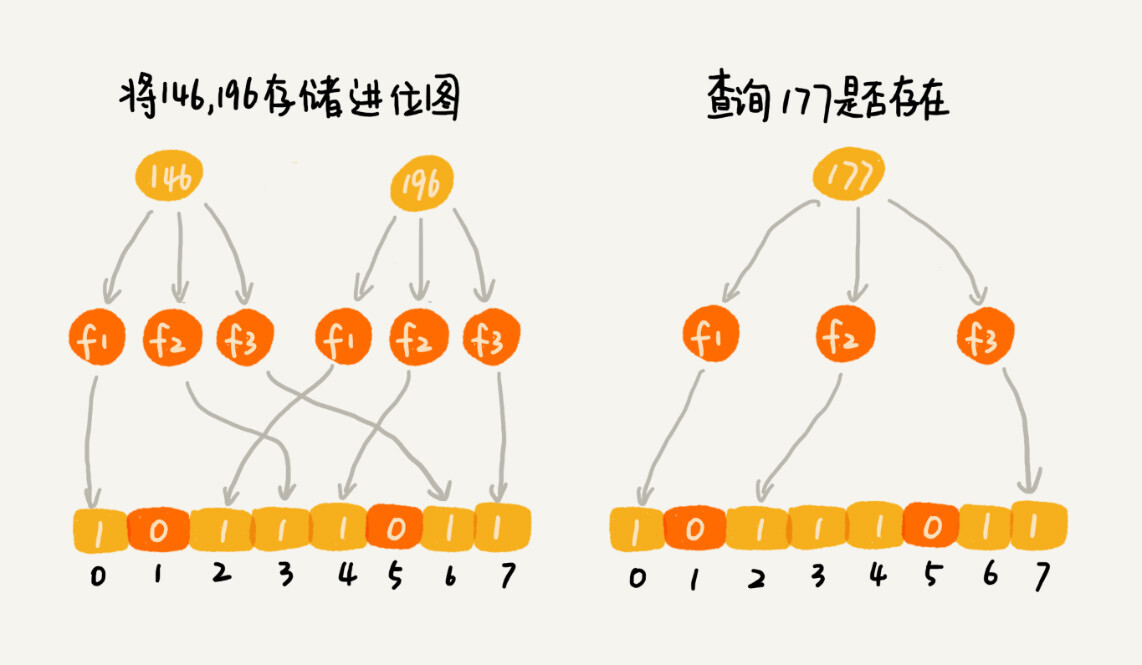
  1. 使用 K 个哈希函数，对同一个数字进行求哈希值，那会得到 K 个不同的哈希值分别记作 X1，X2，X3，…，Xk
  2. 把这 K 个数字作为位图中的下标，将对应的 BitMap[X1]，BitMap[X2]，BitMap[X3]，…，BitMap[Xk]都设置成 true
  3. 用 K 个二进制位，来表示一个数字的存在。当查询某个数字是否存在的时候，用同样的 K 个哈希函数，对这个数字求哈希值，分别得到 Y1，Y2，Y3，…，Yk。
  4. 看这 K 个哈希值，对应位图中的数值是否都为 true，如果都是 true，则说明，这个数字存在，如果有其中任意一个不为 true，那就说明这个数字不存在。

问题：容易误判

尽管布隆过滤器会存在误判，但是，这并不影响它发挥大作用。

布隆过滤器与散列表

布隆过滤器用多个哈希函数对同一个网页链接进行处理，CPU 只需要将网页链接从内存中读取一次，进行多次哈希计算，理论上讲这组操作是 CPU 密集型的。而在散列表的处理方式中，需要读取散列值相同（散列冲突）的多个网页链接，分别跟待判重的网页链接，进行字符串匹配。这个操作涉及很多内存数据的读取，所以是内存密集型的。

CPU 计算可能是要比内存访问更快速的，所以，理论上讲，布隆过滤器的判重方式，更加快速。

查看评论