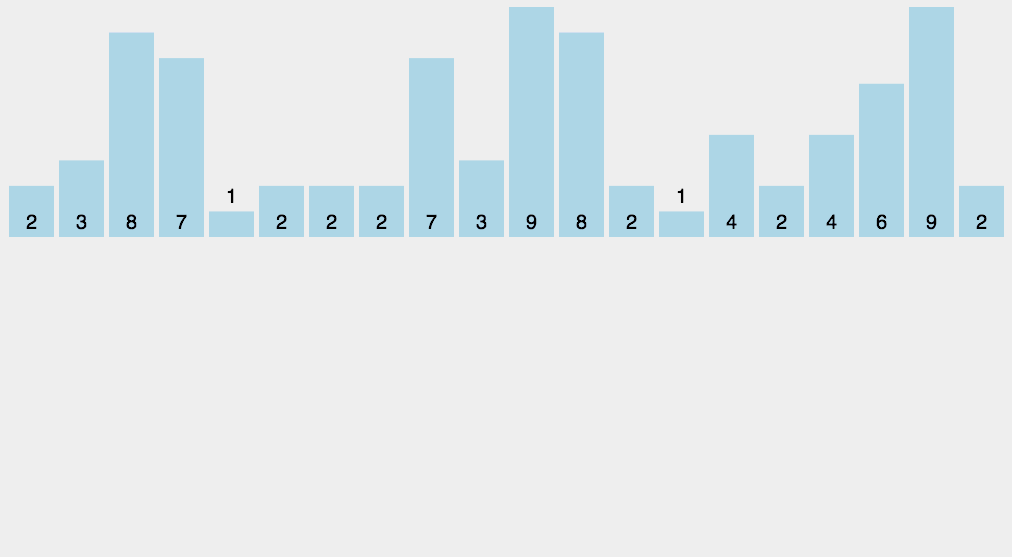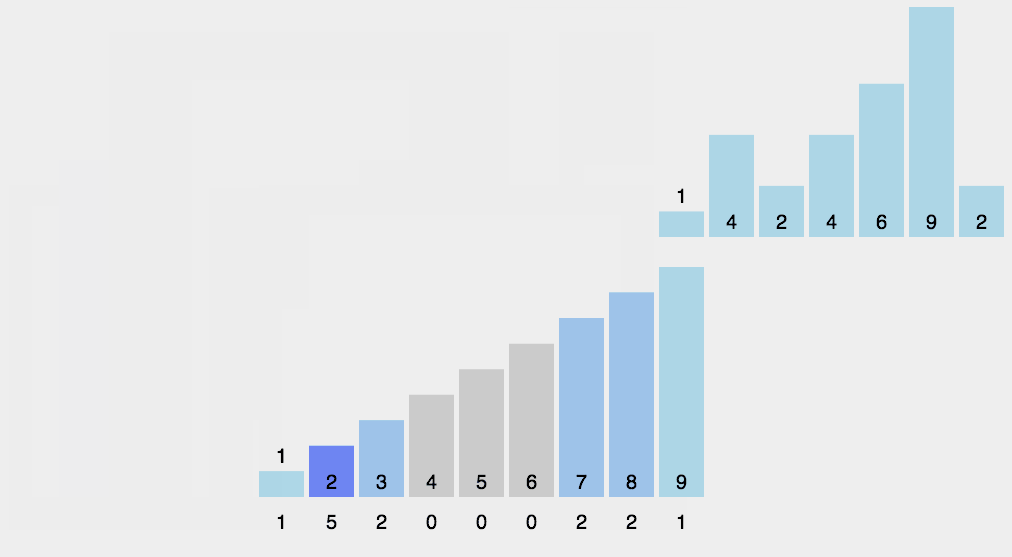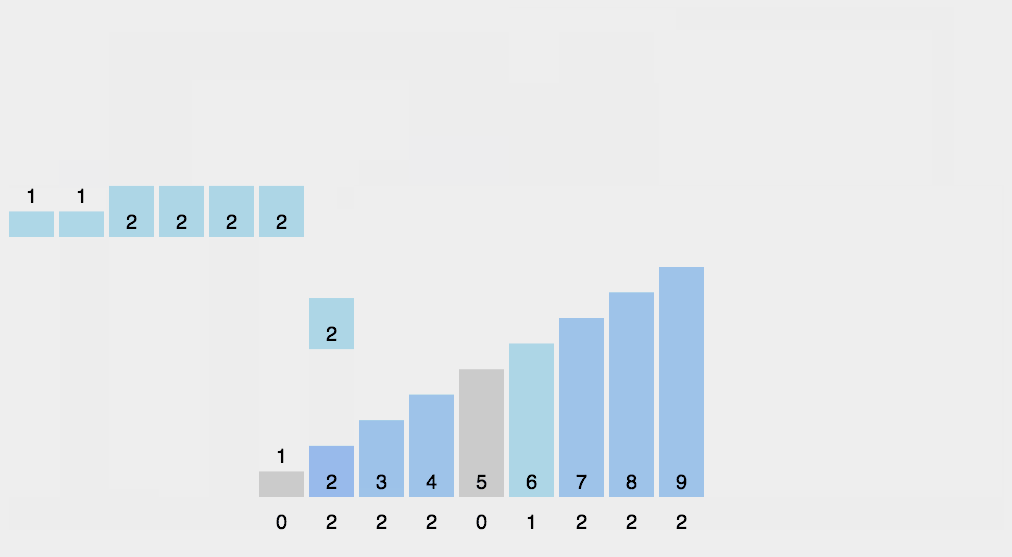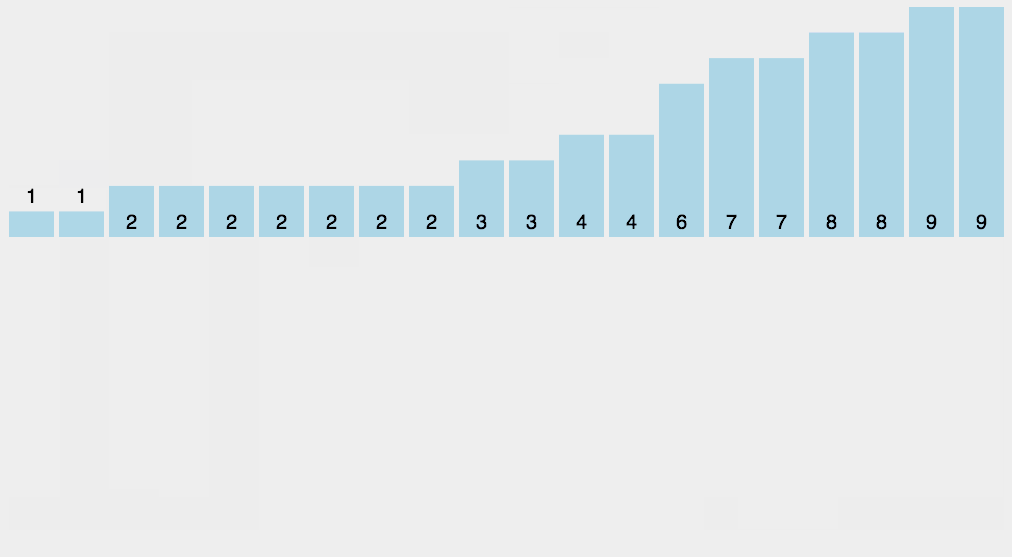排序算法

December 13, 2021 14836

The mystery of creation is like the darkness of night–it is great.

Delusions of knowledge are like the fog of the morning.

https://www.cnblogs.com/l199616j/p/10742603.html#_label0_0

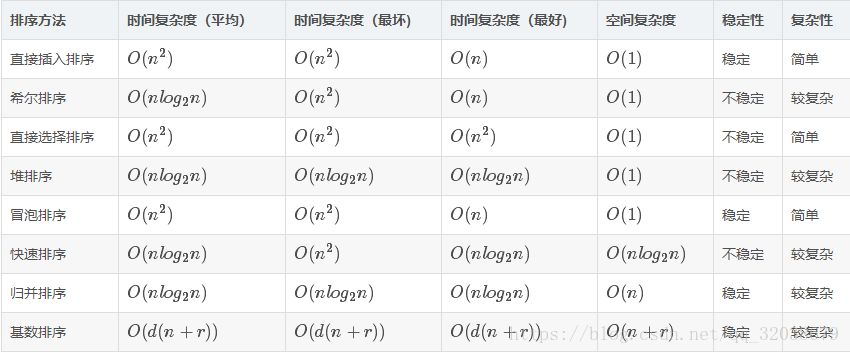
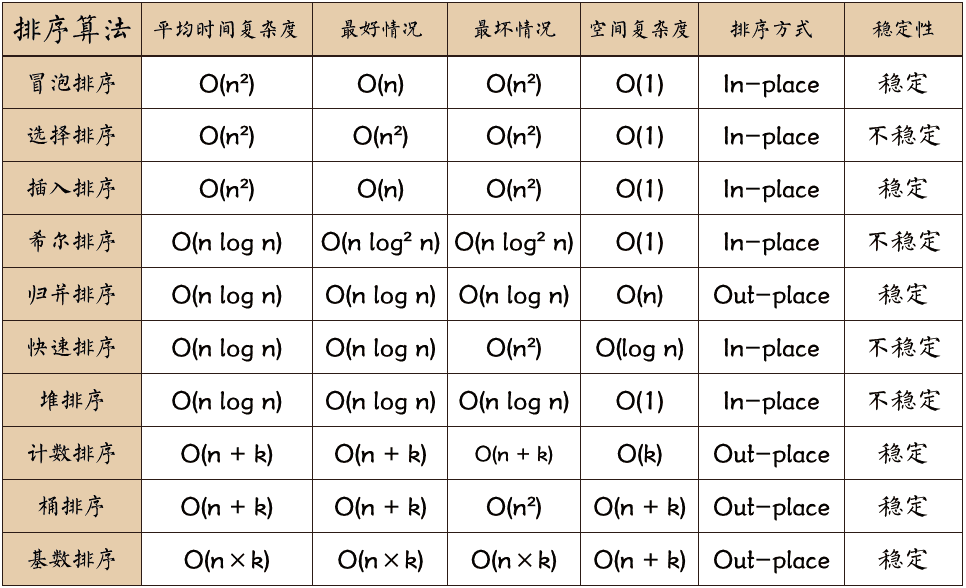
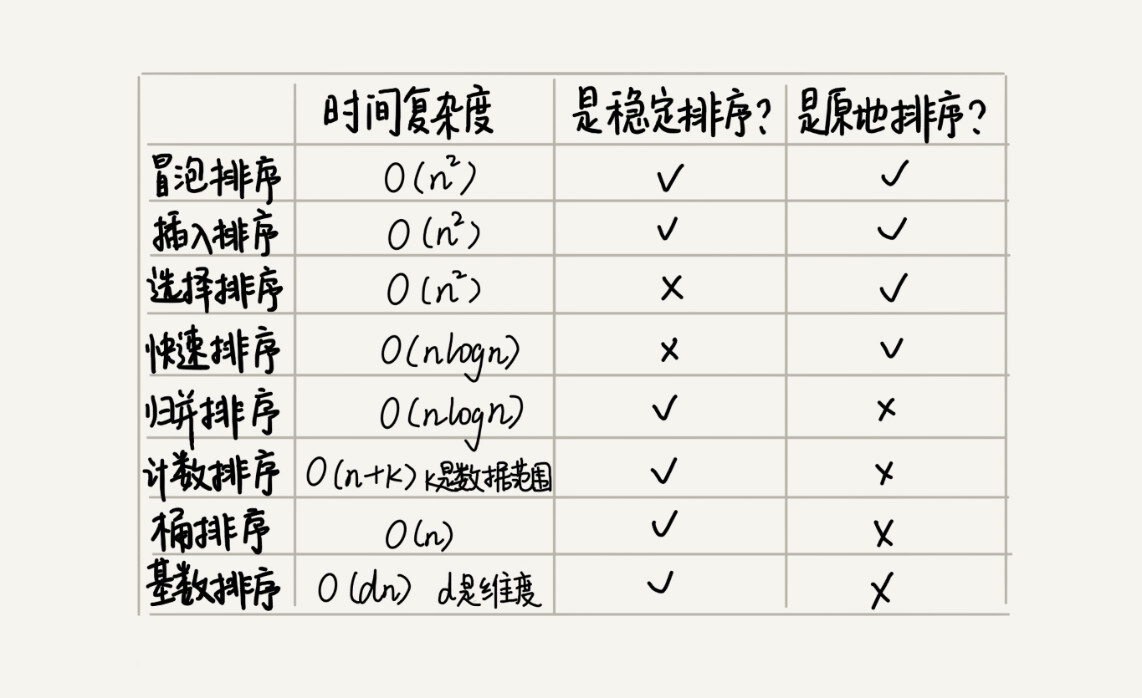
如何分析一个“排序算法”？

排序算法的执行效率

  1. 最好情况、最坏情况、平均情况时间复杂度
  2. 时间复杂度的系数、常数 、低阶
  3. 比较次数和交换（或移动）次数

排序算法的内存消耗

原地排序（Sorted in place）

原地排序算法，就是特指空间复杂度是 O(1) 的排序算法

原地排序算法：冒泡排序、插入排序、选择排序

排序算法的稳定性

稳定性。这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

“有序度”和“逆序度”

有序度是数组中具有有序关系的元素对的个数。

完全有序的数组的有序度叫作满有序度：n*(n-1)/2

逆序度是数组中不具有有序关系的元素对的个数。

逆序度 = 满有序度 - 有序度

冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。

在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，我们不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法。

算法步骤

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们的位置；
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数；
  3. 针对所有的元素重复以上的步骤，除了最后一个；
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

Java算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int[] bubbleSort(int[] array){
  //外层循环 判断循环走多少次
  for(int i = 0; i < array.length - 1; i++){
    //比较相邻的元素。如果第一个比第二个大，就交换他们的位置
    for(int j = 0; j < array.length - 1 - i; j++){
      if(array[j+1] < array[j]){
        int temp = array[j];
        array[j] = array[j+1];
        array[j+1] = temp;
      }
    }
  }
  return array;
}

算法增加标志位改进

  • 增加标志位，减少没有意义的比较
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int[] bubbleSort(int[] array){
  //外层循环 判断循环走多少次
  for(int i = 0; i < array.length - 1; i++){
    //设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成
    boolean flag = true;
    //比较相邻的元素。如果第一个比第二个大，就交换他们的位置
    for(int j = 0; j < array.length - 1 - i; j++){
      if(array[j+1] < array[j]){
        int temp = array[j];
        array[j] = array[j+1];
        array[j+1] = temp;
        //相邻数字排序完成后，置为true
        flag = false;
      }
    }
    //如果其中一轮完全没有进入第二次循环中的置换顺序，说明没有需要置换的相邻元素，那么说明已经不需要再次进行排序，flag为true，可以直接跳出循环
    if(flag){
      break;
    }
  }
  reyurn array;
}

插入排序

插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O(1)，也就是说，这是一个原地排序算法。

在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

选择排序是一种不稳定的排序算法

  1. 首先，我们将数组中的数据分为两个区间，已排序区间和未排序区间。
  2. 初始已排序区间只有一个元素，就是数组的第一个元素。
  3. 插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。
  4. 重复这个过程，直到未排序区间中元素为空，算法结束。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 插入排序，a表示数组，n表示数组大小
public void insertionSort(int[] a, int n) {
  if (n <= 1) return;

  for (int i = 1; i < n; ++i) {
    int value = a[i];
    int j = i - 1;
    // 查找插入的位置
    for (; j >= 0; --j) {
      if (a[j] > value) {
        a[j+1] = a[j];  // 数据移动
      } else {
        break;
      }
    }
    a[j+1] = value; // 插入数据
  }
}

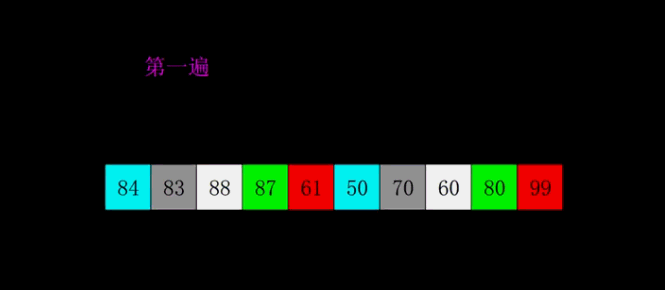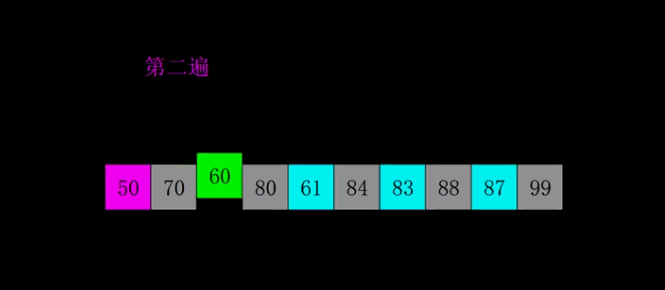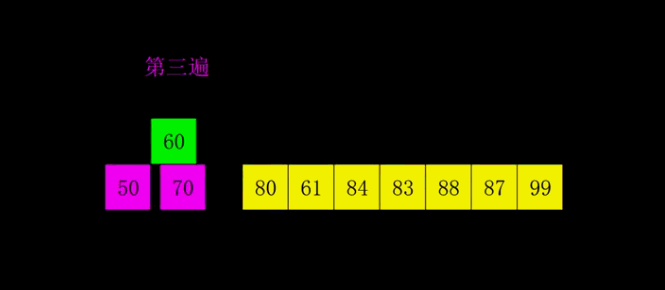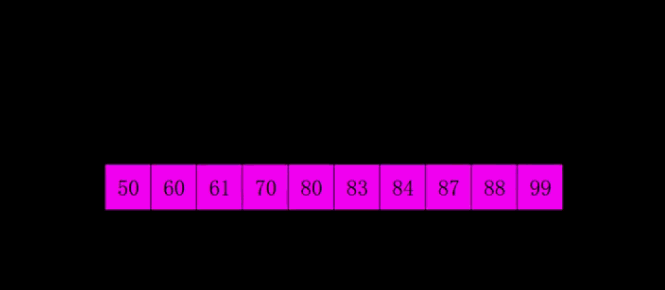
选择排序

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

选择排序空间复杂度为 O(1)，是一种原地排序算法

算法步骤

  1. 第一个跟后面的所有数相比较，如果小于（或等于）第一个数的时候，暂存较小数的下标，第一趟结束后，将第一个数，与暂存的那个最小数进行交换，第一个数就是最小（或最大的数）

  2. 下标移到第二位，第二个数跟后面的所有数相比，一趟下来，确定第二小（或第二大）的数

  3. 重复以上步骤，直到指针移到倒数第二位，确定倒数第二小（或倒数第二大）的数，那么最后一位也就确定了，排序完成。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.Arrays;
public class Main {
  public static void main(String[] args) {
    int[] n = new int[]{1,6,3,8,33,27,66,9,7,88};
    int temp,index = -1;
    for (int i = 0; i < n.length-1; i++) {
      index=i;
      //如果大于，暂存较小的数的下标
      for (int j = i+1; j <n.length; j++) {
        if(n[index]>n[j]){
          index = j;
        }
      }
      ////将一趟下来求出的最小数，与这个数交换
      if(index>0){
        temp = n[i];
        n[i] = n[index];
        n[index] = temp;
      }
      System.out.println(Arrays.toString(n));
    }
    System.out.println(Arrays.toString(n));
  }
}

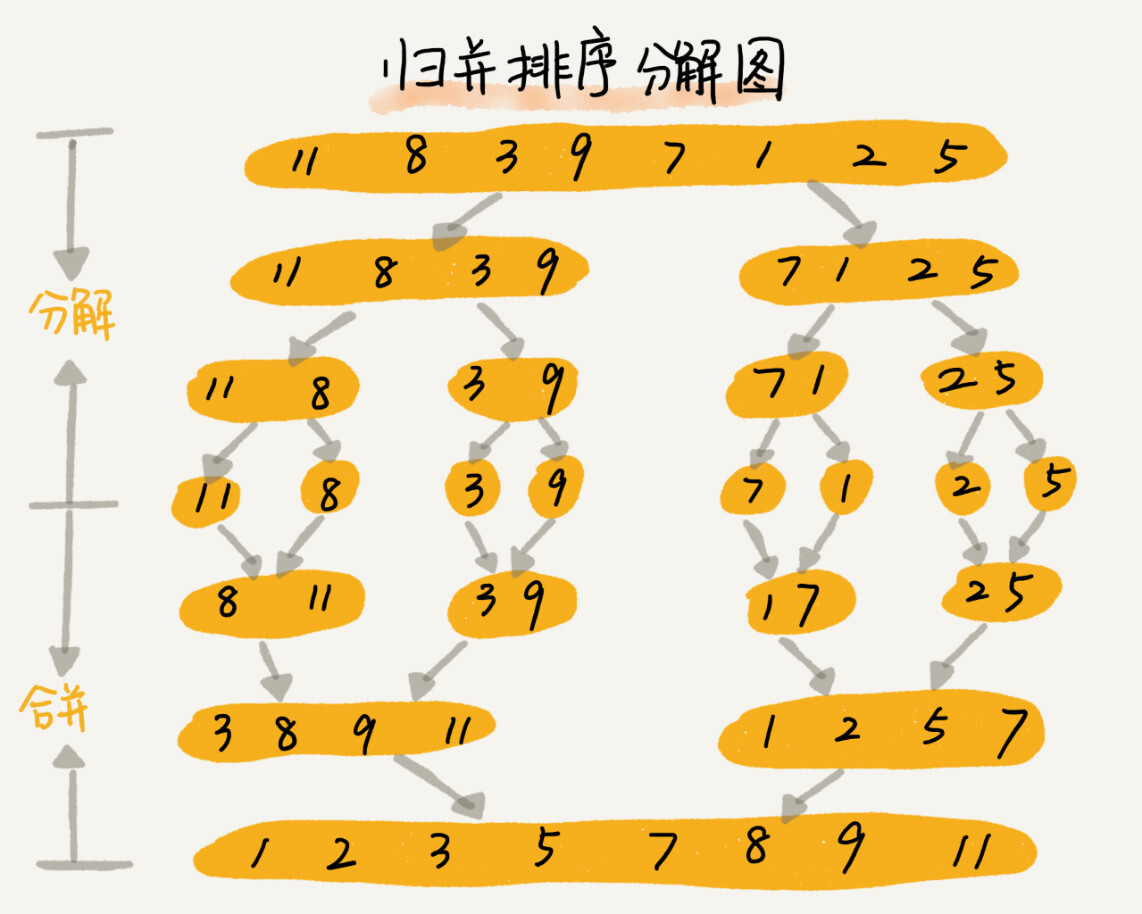
归并排序

核心思想:如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

在合并的过程中，如果 A[p…q]和 A[q+1…r]之间有值相同的元素，先把 A[p…q]中的元素放入 tmp 数组。这样就保证了值相同的元素，在合并前后的先后顺序不变。所以，归并排序是一个稳定的排序算法。

时间复杂度：

T(a) = T(b) + T(c) + K

其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。

我们假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。我们知道，merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是：

T(1) = C； n=1时，只需要常量级的执行时间，所以表示为C。
T(n) = 2*T(n/2) + n； n>1

1
2
3
4
5
6
7
T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......

通过这样一步一步分解推导，我们可以得到 T(n) = 2^kT(n/2^k)+kn。当 T(n/2^k)=T(1) 时，也就是 n/2^k=1，我们得到 k=log2n 。我们将 k 值代入上面的公式，得到 T(n)=Cn+nlog2n 。

如果我们用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。

归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)

空间复杂度是 O(n)

归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。

分治是一种解决问题的处理思想，递归是一种编程技巧

递推公式

1
2
3
4
5
//递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))

//终止条件：
p >= r 不用再继续分解

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import java.util.Arrays;

public class Main {
  public static void main(String[] args) {
    int[] arr = new int[]{3,6,4,7,5,2};
    merge(arr,0,arr.length-1);
    System.out.println(Arrays.toString(arr));
  }

  //归并
  public static void merge(int[] arr,int low,int high){
    int center = (high+low)/2;
    if(low<high){
      //递归，直到low==high，也就是数组已不能再分了，
      merge(arr,low,center);
      merge(arr,center+1,high);

      //当数组不能再分，开始归并排序
      mergeSort(arr,low,center,high);
      System.out.println(Arrays.toString(arr));
    }
  }

  //排序
  public static void mergeSort(int[] arr,int low,int center,int high){
    //用于暂存排序后的数组的临时数组
    int[] tempArr = new int[arr.length];
    int i = low,j = center+1;

    //临时数组的下标
    int index = 0;

    //循环遍历两个数组的数字，将小的插入到临时数组里
    while(i<=center && j<= high){

      //左边数组的数小，插入到新数组
      if(arr[i]<arr[j]){
        tempArr[index] = arr[i];
        i++;
      }else{//右边数组的数小，插入到新数组
        tempArr[index] = arr[j];
        j++;
      }
      index++;
    }

    //处理左半边数组多余的数据，将左半边多余的数据直接追加的临时数组的后面
    while(i<=center){
      tempArr[index] = arr[i];
      i++;
      index++;
    }

    //处理右半边数组多余的数据，将右半边多余的数据直接追加的临时数组的后面
    while(j<= high){
      tempArr[index] = arr[j];
      j++;
      index++;
    }

    //将临时数组中的数据重新放进原数组
    for (int k = 0; k < index; k++) {
      arr[k+low] = tempArr[k];
    }
  }
}

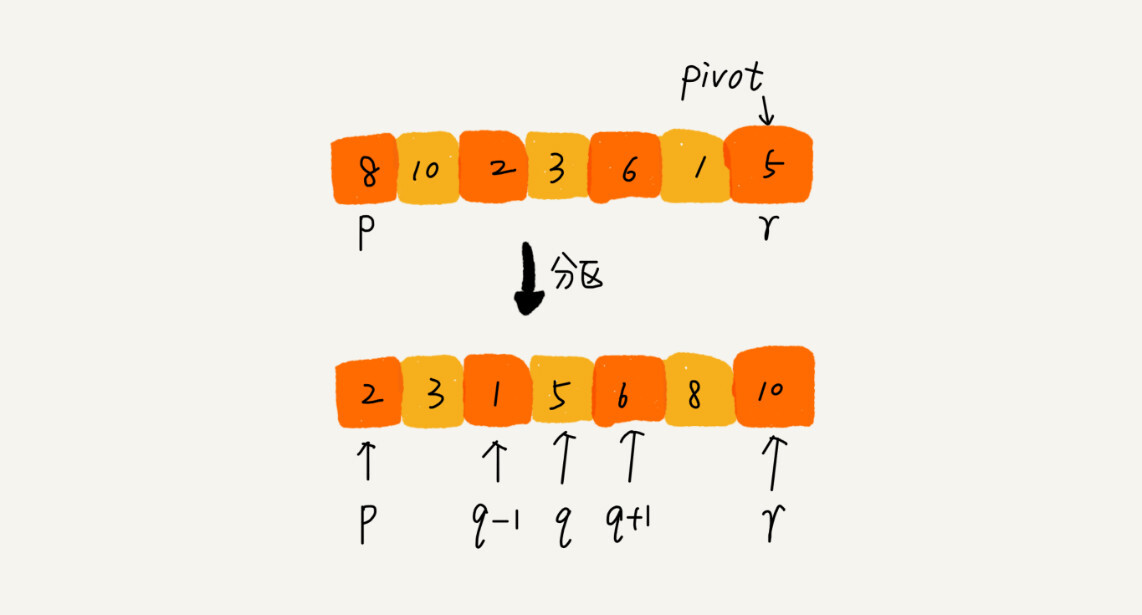
快速排序

快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

快排是一种原地、不稳定的排序算法

时间复杂度：

快排的时间复杂度递推求解公式跟归并是相同的。所以，快排的时间复杂度也是 O(nlogn)。

T(1) = C； n=1时，只需要常量级的执行时间，所以表示为C。
T(n) = 2*T(n/2) + n； n>1

公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。

最坏情况时间复杂度:O(n2)

T(n) 在大部分情况下的时间复杂度都可以做到 O(nlogn)，只有在极端情况下，才会退化到 O(n2)

递推公式

1
2
3
4
5
6

//递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)

//终止条件：
p >= r

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class QuickSort {

  // 快速排序，a是数组，n表示数组的大小
  public static void quickSort(int[] a, int n) {
    quickSortInternally(a, 0, n-1);
  }

  // 快速排序递归函数，p,r为下标
  private static void quickSortInternally(int[] a, int p, int r) {
    if (p >= r) return;

    int q = partition(a, p, r); // 获取分区点
    quickSortInternally(a, p, q-1);
    quickSortInternally(a, q+1, r);
  }

  private static int partition(int[] a, int p, int r) {
    int pivot = a[r];
    int i = p;
    for(int j = p; j < r; ++j) {
      if (a[j] < pivot) {
        if (i == j) {
          ++i;
        } else {
          int tmp = a[i];
          a[i++] = a[j];
          a[j] = tmp;
        }
      }
    }

    int tmp = a[i];
    a[i] = a[r];
    a[r] = tmp;

    System.out.println("i=" + i);
    return i;
  }
}

优化快速排序

为什么最坏情况下快速排序的时间复杂度是 O(n2) 呢？

如果数据原来就是有序的或者接近有序的，每次分区点都选择最后一个数据，那快速排序算法就会变得非常糟糕，时间复杂度就会退化为 O(n2)。实际上，这种 O(n2) 时间复杂度出现的主要原因还是因为我们分区点选得不够合理。

最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。

  1. 三数取中法

    从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。

    这样每间隔某个固定的长度，取数据出来比较，将中间值作为分区点的分区算法，肯定要比单纯取某一个数据更好。

    但是，如果要排序的数组比较大，那“三数取中”可能就不够了，可能要“五数取中”或者“十数取中”。

  2. 随机法

    随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好，但是从概率的角度来看，也不大可能会出现每次分区点都选得很差的情况，所以平均情况下，这样选的分区点是比较好的。时间复杂度退化为最糟糕的 O(n2) 的情况，出现的可能性不大。

警惕堆栈溢出

为了避免快速排序里，递归过深而堆栈过小，导致堆栈溢出，我们有两种解决办法：

  1. 第一种是限制递归深度。一旦递归过深，超过了我们事先设定的阈值，就停止递归。
  2. 第二种是通过在堆上模拟实现一个函数调用栈，手动模拟递归压栈、出栈的过程，这样就没有了系统栈大小的限制。

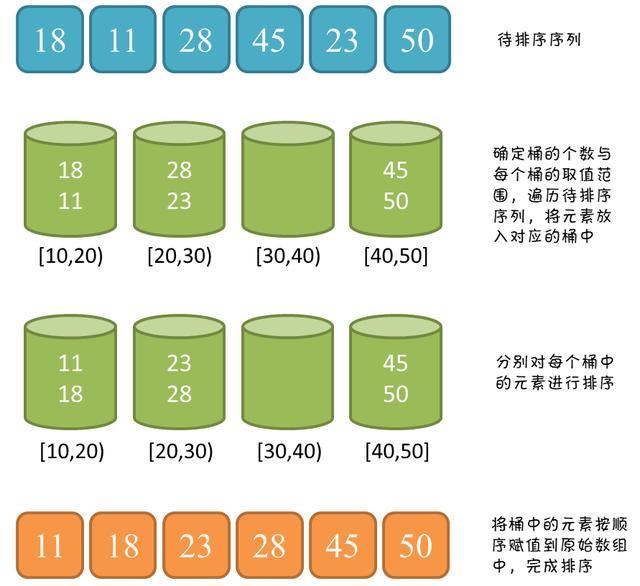
桶排序

核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

桶排序的时间复杂度是 O(n)

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。

每个桶内部使用快速排序，时间复杂度为 O(k logk)。m 个桶排序的时间复杂度就是 O(m k logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(nlog(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

桶排序对要排序数据的要求是非常苛刻的:

  1. 首先，要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
  2. 其次，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
public class BucketSort {

  /**
     * 桶排序
     *
     * @param arr 数组
     * @param bucketSize 桶容量
     */
  public static void bucketSort(int[] arr, int bucketSize) {
    if (arr.length < 2) {
      return;
    }

    // 数组最小值
    int minValue = arr[0];
    // 数组最大值
    int maxValue = arr[1];
    for (int i = 0; i < arr.length; i++) {
      if (arr[i] < minValue) {
        minValue = arr[i];
      } else if (arr[i] > maxValue) {
        maxValue = arr[i];
      }
    }

    // 桶数量
    int bucketCount = (maxValue - minValue) / bucketSize + 1;
    int[][] buckets = new int[bucketCount][bucketSize];
    int[] indexArr = new int[bucketCount];

    // 将数组中值分配到各个桶里
    for (int i = 0; i < arr.length; i++) {
      int bucketIndex = (arr[i] - minValue) / bucketSize;
      if (indexArr[bucketIndex] == buckets[bucketIndex].length) {
        ensureCapacity(buckets, bucketIndex);
      }
      buckets[bucketIndex][indexArr[bucketIndex]++] = arr[i];
    }

    // 对每个桶进行排序，这里使用了快速排序
    int k = 0;
    for (int i = 0; i < buckets.length; i++) {
      if (indexArr[i] == 0) {
        continue;
      }
      quickSortC(buckets[i], 0, indexArr[i] - 1);
      for (int j = 0; j < indexArr[i]; j++) {
        arr[k++] = buckets[i][j];
      }
    }
  }

  /**
     * 数组扩容
     *
     * @param buckets
     * @param bucketIndex
     */
  private static void ensureCapacity(int[][] buckets, int bucketIndex) {
    int[] tempArr = buckets[bucketIndex];
    int[] newArr = new int[tempArr.length * 2];
    for (int j = 0; j < tempArr.length; j++) {
      newArr[j] = tempArr[j];
    }
    buckets[bucketIndex] = newArr;
  }

  /**
     * 快速排序递归函数
     *
     * @param arr
     * @param p
     * @param r
     */
  private static void quickSortC(int[] arr, int p, int r) {
    if (p >= r) {
      return;
    }

    int q = partition(arr, p, r);
    quickSortC(arr, p, q - 1);
    quickSortC(arr, q + 1, r);
  }

  /**
     * 分区函数
     *
     * @param arr
     * @param p
     * @param r
     * @return 分区点位置
     */
  private static int partition(int[] arr, int p, int r) {
    int pivot = arr[r];
    int i = p;
    for (int j = p; j < r; j++) {
      if (arr[j] <= pivot) {
        swap(arr, i, j);
        i++;
      }
    }

    swap(arr, i, r);
    return i;
  }

  /**
     * 交换
     *
     * @param arr
     * @param i
     * @param j
     */
  private static void swap(int[] arr, int i, int j) {
    if (i == j) {
      return;
    }

    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }
}

计数排序

计数排序其实是桶排序的一种特殊情况

当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

// 计数排序，a是数组，n是数组大小。假设数组中存储的都是非负整数。
public void countingSort(int[] a, int n) {
  if (n <= 1) return;

  // 查找数组中数据的范围
  int max = a[0];
  for (int i = 1; i < n; ++i) {
    if (max < a[i]) {
      max = a[i];
    }
  }

  int[] c = new int[max + 1]; // 申请一个计数数组c，下标大小[0,max]
  for (int i = 0; i <= max; ++i) {
    c[i] = 0;
  }

  // 计算每个元素的个数，放入c中
  for (int i = 0; i < n; ++i) {
    c[a[i]]++;
  }

  // 依次累加
  for (int i = 1; i <= max; ++i) {
    c[i] = c[i-1] + c[i];
  }

  // 临时数组r，存储排序之后的结果
  int[] r = new int[n];
  // 计算排序的关键步骤，有点难理解
  for (int i = n - 1; i >= 0; --i) {
    int index = c[a[i]]-1;
    r[index] = a[i];
    c[a[i]]--;
  }

  // 将结果拷贝给a数组
  for (int i = 0; i < n; ++i) {
    a[i] = r[i];
  }
}

基数排序

先按照最后一位来排序手机号码，然后，再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。

这里按照每位来排序的排序算法要是稳定的

基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。

实现算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class RadixSort {

  /**
     * 基数排序
     *
     * @param arr
     */
  public static void radixSort(int[] arr) {
    int max = arr[0];
    for (int i = 0; i < arr.length; i++) {
      if (arr[i] > max) {
        max = arr[i];
      }
    }

    // 从个位开始，对数组arr按"指数"进行排序
    for (int exp = 1; max / exp > 0; exp *= 10) {
      countingSort(arr, exp);
    }
  }

  /**
     * 计数排序-对数组按照"某个位数"进行排序
     *
     * @param arr
     * @param exp 指数
     */
  public static void countingSort(int[] arr, int exp) {
    if (arr.length <= 1) {
      return;
    }

    // 计算每个元素的个数
    int[] c = new int[10];
    for (int i = 0; i < arr.length; i++) {
      c[(arr[i] / exp) % 10]++;
    }

    // 计算排序后的位置
    for (int i = 1; i < c.length; i++) {
      c[i] += c[i - 1];
    }

    // 临时数组r，存储排序之后的结果
    int[] r = new int[arr.length];
    for (int i = arr.length - 1; i >= 0; i--) {
      r[c[(arr[i] / exp) % 10] - 1] = arr[i];
      c[(arr[i] / exp) % 10]--;
    }

    for (int i = 0; i < arr.length; i++) {
      arr[i] = r[i];
    }
  }
}

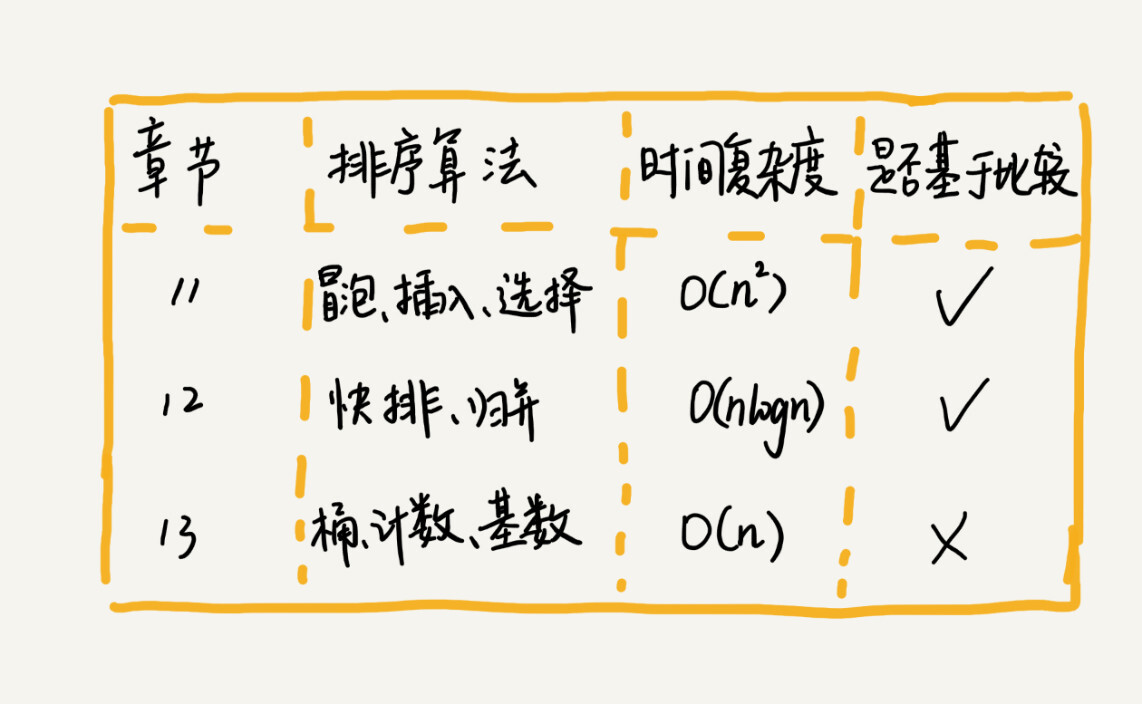
希尔排序

堆排序

排序优化：如何实现一个通用的、高性能的排序函数？

线性排序算法的时间复杂度比较低，适用场景比较特殊。所以如果要写一个通用的排序函数，不能选择线性排序算法。

如果对小规模数据进行排序，可以选择时间复杂度是 O(n2) 的算法；如果对大规模数据进行排序，时间复杂度是 O(nlogn) 的算法更加高效。

举例分析排序函数

qsort() 会优先使用归并排序来排序输入数据，因为归并排序的空间复杂度是 O(n)，所以对于小数据量的排序问题不大。

但要排序的数据量比较大的时候，qsort() 会改为用快速排序算法来排序。qsort() 是通过自己实现一个堆上的栈，手动模拟递归来解决的。

实际上，qsort() 并不仅仅用到了归并排序和快速排序，它还用到了插入排序。在快速排序的过程中，当要排序的区间中，元素的个数小于等于 4 时，qsort() 就退化为插入排序，不再继续用递归来做快速排序，因为在小规模数据面前，O(n2) 时间复杂度的算法并不一定比 O(nlogn) 的算法执行时间长。

查看评论