二分查找
二分查找
二分查找(Binary Search)算法,也叫折半查找算法
二分查找针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。
时间复杂度:O(logn)
假设数据大小是 n,每次查找后数据都会缩小为原来的一半,也就是会除以 2。最坏情况下,直到查找区间被缩小为空,才停止。

其中 n/2k=1 时,k 的值就是总共缩小的次数。
而每一次缩小操作只涉及两个数据的大小比较,所以,经过了 k 次区间缩小操作,时间复杂度就是 O(k)。
通过 n/2k=1,我们可以求得 k=log2n,所以时间复杂度就是 O(logn)。
指数时间复杂度的算法在大规模数据面前是无效的
二分查找的递归与非递归实现
非递归实现
有序数组中不存在重复元素,用二分查找值等于给定值的数据
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
//int mid = (low + high) / 2;
int mid = low+(high-low)/2;
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}
注意:
注意是 low<=high,而不是 <
mid=(low+high)/2 这种写法是有问题的。
因为如果 low 和 high 比较大的话,两者之和就有可能会溢出。
改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步,如果要将性能优化到极致的话,我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说,计算机处理位运算要快得多。
low 和 high 的更新
low=mid+1,high=mid-1
递归实现
1 | |
二分查找应用场景的局限性
首先,二分查找依赖的是顺序表结构,简单点说就是数组。
二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的,则无法应用二分查找。
其次,二分查找针对的是有序数据。
二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中
再次,数据量太小不适合二分查找。
例外:如果数据之间的比较操作非常耗时,不管数据量大小,推荐使用二分查找。比如,数组中存储的都是长度超过 300 的字符串,如此长的两个字符串之间比对大小,就会非常耗时。我们需要尽可能地减少比较次数,而比较次数的减少会大大提高性能,这个时候二分查找就比顺序遍历更有优势。
最后,数据量太大也不适合二分查找。
二分查找变形问题
查找第一个值等于给定值的元素
问题:有序数据集合中存在重复的数据,希望找到第一个值等于给定值的数据
下面这样一个有序数组,其中,a[5],a[6],a[7]的值都等于 8,是重复的数据。希望查找第一个等于 8 的数据,也就是下标是 5 的元素。

2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33//写法一:
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
high = mid - 1;
} else {
low = mid + 1;
}
}
if (low < n && a[low]==value) return low;
else return -1;
}
//写法二:
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == 0) || (a[mid - 1] != value)) return mid;
else high = mid - 1;
}
}
return -1;
}
查找最后一个值等于给定值的元素
问题:有序数据集合中存在重复的数据,希望查找最后一个值等于给定值的元素
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
else low = mid + 1;
}
}
return -1;
}
查找第一个大于等于给定值的元素
问题:在有序数组中,查找第一个大于等于给定值的元素
数组中存储的这样一个序列:3,4,6,7,10。如果查找第一个大于等于 5 的元素,那就是 6。
2
3
4
5
6
7
8
9
10
11
12
13
14public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
if ((mid == 0) || (a[mid - 1] < value)) return mid;
else high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
查找最后一个小于等于给定值的元素
问题:查找最后一个小于等于给定值的元素
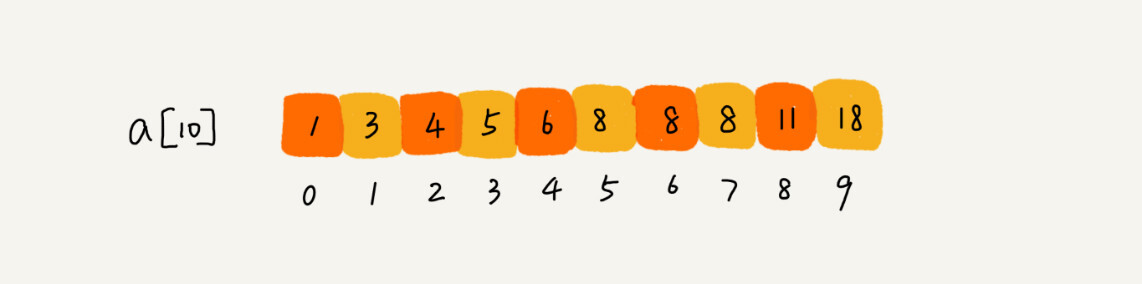
数组中存储了这样一组数据:3,5,6,8,9,10。最后一个小于等于 7 的元素就是 6
2
3
4
5
6
7
8
9
10
11
12
13
14public int bsearch7(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else {
if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
else low = mid + 1;
}
}
return -1;
}
LeetCode实战经验
target 是在一个在左闭右闭的区间,[left, right]
left = 0;
right = nums.length - 1;二分细节
循环体:当left==right,区间[left, right]依然有效,所以用 <=
1
while (left <= right){};target 在左区间
1
right = middle - 1;target 在右区间
1
left = middle + 1;target 是在一个在左闭右开的区间里,[left, right)
left = 0;
right = nums.length;二分细节
循环体:因为left == right的时候,在[left, right)是无效的空间,所以使用 <
1
while (left < right){};target 在左区间
1
right = middle;target 在右区间
1
left = middle + 1;
Leetcode实战
先找到位置,遍历左右
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
if(len == 0 || nums[0] > target || nums[len-1] < target){
return new int[]{-1,-1};
}
int result = -1;
result = binarySearch(nums,target);
if(result != -1){
int left = result;
int right = result;
while(left - 1 >= 0 && nums[left-1] == target ){
left--;
}
while(right + 1 < len && nums[right+1] == target ){
right++;
}
return new int[]{left,right};
}else{
return new int[]{-1,-1};
}
}
public int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length;
while(left < right){
int mid = left + (right - left)/2;
if(nums[mid] > target){
right = mid;
}else if(nums[mid] < target){
left = mid + 1;
}else{
return mid;
}
}
return -1;
}
}直接找到左右边界
寻找右边界(不包括target)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15int getRightBorder(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] > target) {
right = middle - 1;
} else { // 寻找右边界,nums[middle] == target的时候更新left
left = middle + 1;
rightBorder = left;
}
}
return rightBorder;
}寻找左边界(不包括target)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15int getLeftBorder(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
right = middle - 1;
leftBorder = right;
} else {
left = middle + 1;
}
}
return leftBorder;
}主函数
1
2
3
4
5
6
7int[] searchRange(int[] nums, int target) {
int leftBorder = getLeftBorder(nums, target);
int rightBorder = getRightBorder(nums, target);
if (leftBorder == -2 || rightBorder == -2) return new int[]{-1, -1};
if (rightBorder - leftBorder > 1) return new int[]{leftBorder + 1, rightBorder - 1};
return new int[]{-1, -1};
}
1 | |
- 本文作者:bobo
- 本文链接:https://boyolo.github.io/article/42877.html
- 版权声明:本博客所有文章均采用 BY-NC-SA 许可协议,转载请注明出处!